백준 2747번 피보나치 수
December 16, 2020
Description
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다.
이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가 된다.
n=17일때 까지 피보나치 수를 써보면 다음과 같다.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
n이 주어졌을 때, n번째 피보나치 수를 구하는 프로그램을 작성하시오.Input
첫째 줄에 n이 주어진다. n은 45보다 작거나 같은 자연수이다.Output
첫째 줄에 n번째 피보나치 수를 출력한다.Solution
# 내 풀이
n = int(input())
def fibonacci(n):
if n>1:
answer = fibonacci(n-1) + fibonacci(n-2)
else: answer = n
return answer
print(fibonacci(n))시간 초과 판정을 받았다.
Feedback
- 재귀적으로 피보나치 수열을 구현하면 동일한 함수가 여러 번 호출된다.
- 예를 들어 fib(5)를 호출할 경우 fib(1)은 5번이나 호출된다.
- 재귀적으로 구현할 때의 시간복잡도는 이다.
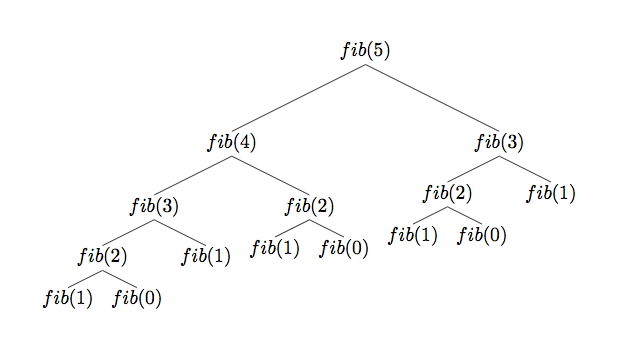
따라서 아래와 같이 재귀적인 개념을 빌려오지만 재귀함수는 호출하지 않는 방식으로 구현해야 한다.
# 다른 사람 풀이
n = int(input())
a, b = 0, 1
while n > 0:
a, b = b, a + b
n -= 1
print(a)Source
