이코테 Chapter 8 다이나믹 프로그래밍

February 08, 2021

다이나믹 프로그래밍(Dynamic Programming)

연속적이지 않은 데이터에 대해 메모이제이션 기법을 사용하는 경우 배열이나 리스트가 아닌 사전(dict) 자료형을 이용하는 게 더 효과적이다.
완전 탐색으로 접근했을 때 시간 초과가 뜬다면 다이나믹 프로그래밍으로 해결할 수 있는지 부분 문제들의 중복 여부를 확인해보는 것이 좋다.
재귀함수를 이용한 탑다운 방식보다는 보텀업 방식으로 구현하는 것이 좋지만, 재귀함수로 구현했다면 sys 라이브러리의 setrecursionlimit() 메서드를 이용해 재귀 제한을 완화할 수 있다.

>>> import sys
>>> sys.getrecursionlimit()
1000
>>> sys.setrecursionlimit(2000)    # 최대 재귀호출 횟수를 2000으로 늘림

실전 문제 1: 1로 만들기

Testcase

26
# 3

Solution

쉬운 문제인데 혼자 힘으로 못 풀었다. 언제쯤 혼자 힘으로 DP 문제를 풀 수 있을까?
2시간 동안 고민하다가 풀이를 봤는데 잘 이해가 안 되어 python tutor를 보고 겨우 이해했다.
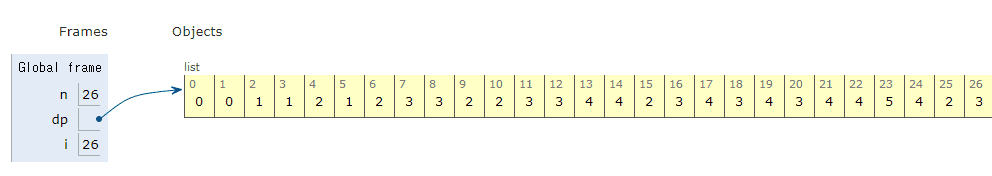
점화식을 잘 세워보자.

n = int(input())

dp = [0] * 30001

for i in range(2, n + 1):
    dp[i] = dp[i - 1] + 1

    if i % 2 == 0:
        dp[i] = min(dp[i], dp[i // 2] + 1)
    if i % 3 == 0:
        dp[i] = min(dp[i], dp[i // 3] + 1)
    if i % 5 == 0:
        dp[i] = min(dp[i], dp[i // 5] + 1)

print(dp[n])

실전 문제 2: 개미 전사

Testcase 1

4
1 3 1 5
# 8

Testcase 2

6
2 4 3 5 8 4
# 13

Solution

오래 고민했지만 또 혼자 힘으로 못 풀었다.
30문제쯤 풀면 익숙해지겠지… 너무 좌절하지 말자.
1로 만들기보다는 개미 전사가 쉬웠다.

n = int(input())

data = list(map(int, input().split()))

dp = [0] * 100

dp[0] = data[0]
dp[1] = max(data[0], data[1])

for i in range(2, n):
    dp[i] = max(dp[i - 1], dp[i - 2] + data[i])

print(dp[n - 1])

실전 문제 3: 바닥 공사

Testcase 1

3
# 5

Testcase 2

7
# 85

Solution

난이도가 쉬운 문제지만 처음으로 혼자 힘으로 푼 DP 문제이다.
여러 경우의 수를 생각해보고, 개미 전사 문제를 응용하니 풀 수 있었다.

n = int(input())

dp = [0] * 1001

dp[1] = 1
dp[2] = 3

for i in range(3, n + 1):
    dp[i] = (dp[i - 2] * 2 + dp[i - 1]) % 796796

print(dp[n])

실전 문제 4: 효율적인 화폐 구성

Testcase 1

Testcase 2

Testcase 3

Solution

그리디 알고리즘과 비슷해 보이지만 큰 화폐가 작은 화폐의 배수가 아니어서 그리디 알고리즘으로 풀 수 없다.
금액을 dp 배열의 인덱스로 두고, 가장 적은 금액부터 차례로 동전의 수를 업데이트하여 저장하면 되겠다는 생각까지는 했는데 구현에 실패했다.
풀이를 이해한 뒤, 다시 풀어보았다. 겨우 이해했지만, 예전보다는 조금 더 익숙해졌다. dp 배열을 0이 아닌 다른 수로 초기화해야 min함수를 사용하여 최솟값을 구할 수 있다는 점을 배웠다.

n, m = map(int, input().split())
money = [int(input()) for _ in range(n)]

dp = [10001] * (m + 1)

dp[0] = 0
for i in range(n):
    for j in range(money[i], m + 1):
        dp[j] = min(dp[j], dp[j - money[i]] + 1)

print(-1) if dp[m] == 10001 else print(dp[m])

Source

Written by@[Jisun Lim]

Carpe diem

GitHub Velog Facebook