복잡도

• 알고리즘의 성능을 나타내는 척도

  • 시간복잡도: 특정한 크기의 입력에 대하여 알고리즘이 얼마나 오래 걸리는지
  • 공간복잡도: 특정한 크기의 입력에 대하여 알고리즘이 얼마나 많은 메모리를 차지하는지
• 동일한 기능을 수행한다면 복잡도가 낮을 수록 좋은 알고리즘이다.

• 복잡도의 측정을 통해 얻을 수 있는 것

  • 시간복잡도: 알고리즘을 위해 필요한 연산의 횟수
  • 공간복잡도: 알고리즘을 위해 필요한 메모리의 양

• 시간복잡도와 공간복잡도는 Trade-off가 성립

  • e.g. Memoization: 메모리를 많이 사용해서 시간을 비약적으로 단축하는 기법

시간 복잡도(Time complextiy)

• 시간복잡도 = 효율성 = 성능
• 각 연산이 수행되는데 몇 단계가 필요한지 측정
• Tip! steps라는 변수를 추가하여 단계수를 기록하면 시간복잡도 증명 가능

O (Big-O)

• 시간의 상한 (upper bound)
• $f(n) = O(g(n))$
  → $f(n)$의 상한은 $g(n)$
  → $f(n)$의 growth rate<= $g(n)$의 growth rate

$O(1)$

• 상수 시간(constant time)

$O(log n)$

• 로그 시간(log time)

• 데이터가 두 배로 증가할 때마다 한 단계씩 늘어나는 알고리즘

  • logarithm = log
  • 지수와 역의 관계

$O(n)$

• 선형 시간(linear time)

def is_prime(number):
	for i in range(2, number):
		if number % i == 0:
			return False
	return True

function hasDuplicateValue(array) {
  var existingNumbers = []
  for (var i = 0; i < array.length; i++) {
    if (existingNumbers[array[i]] === undefined) {
      existingNumbers[array[i]] = 1
    } else {
      return true
    }
  }
  return false
}

$O(nlogn)$

• 로그 선형 시간

$O(n^2)$

• 이차 시간(quadratic time)

$O(n^3)$

• 삼차 시간 (코딩테스트에서는 피하는 것이 좋음)

$O(2^n)$

• 지수 시간

Ω (Big-Omega)

• 시간의 하한 (lower bound)

θ (Big-Theta)

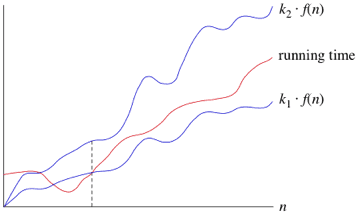
• 점근적으로 근접한 한계값
• $f(n)$ = $θ(g(n))$
  → $n$이 충분히 크다면 실행 시간이 어떤 상수 k1과 k2에 대하여 최소 $k1*g(n)$이며 최대 $k2*g(n)$이 된다는 뜻

연습문제

• if $f(n) = O(g(n))$ and $f(n) = Ω(g(n))$, then we have $(f(n))^2 = Θ(g(n)^2)$ true
• if $f(n) = O(g(n))$ and $f(n) = Ω(g(n))$, then we have $f(n) = g(n)$ false
• 3498103948 = Θ(1)
• log2^n = nlog2 = Θ(n)
• 4n^3 + 2n^log n = Θ(n^log n)
• log2^(3n^4 - 5n^2 + 4) = Θ(n^4)
• T(n) = 2 * T(n-1), T(0) = 1 T(n) = Θ(2^n)

• factorial 메소드의 시간복잡도를 구하여라

  int factorial(int n) {
  	if (n ==1)
  		return 1;
  	else
  		return n * factorial(n-1)
  }

  T(n) = O(1) + (n-1) * O(1) = O(n)

🍯 Tip!

$log n < n < n log n < n^2 < 2^n < 100^n < n! < n^n$

다항함수 < 지수함수 < 팩토리얼 < $n^n$

시간 측정

• 시간 측정

import time
start_time = time.time() # 측정 시작
...
프로그램 소스코드
...
end_time = time.time() # 측정 죵로
print("time: ", end_time - start_time) # 수행 시간 출력

🍯 Tip!

• 시간 제한이 1초일 때 N의 범위 별로 아래의 시간 복잡도인 알고리즘을 설계하면 문제를 풀 수 있다.

  • N의 범위가 500인 경우: $O(n^3)$
  • N의 범위가 2,000인 경우: $O(n^2)$
  • N의 범위가 100,000인 경우: $O(nlogn)$
  • N의 범위가 10,000,000인 경우: $O(n)$

Source

• A Common-Sense Guide to Data Structures and Algorithms
• khanacademy
• Data Structures and Algorithms in Java
• 이것이 취업을 위한 코딩테스트다 with 파이썬